Metropolis-Hastings Monte Carlo Integration
October 25, 2013 - 2:47 pm by Joss Whittle Matlab PhD UniversityA little update on what I’ve been learning about lately.
Metropolis-Hastings is an algorithm for sampling random values out of a probability distribution. Effectively, for a function f(x) you wish to simulate where the curve is higher it is more probable that a random number will be chosen from there. Uniform sampling of the range would mean that all x values on the graph have an even probability of being chosen, this could be simulated by saying f(x) = 1.
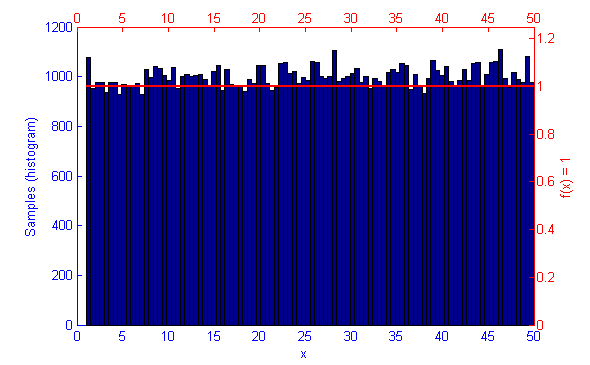
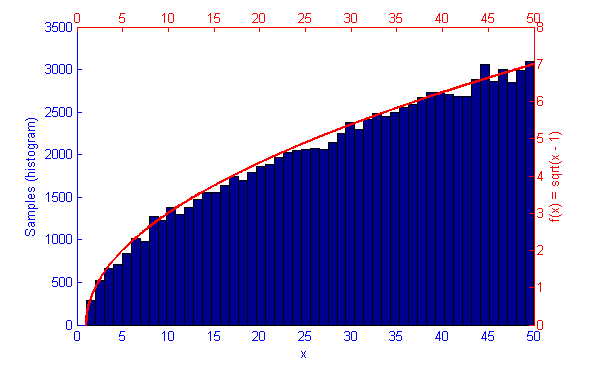
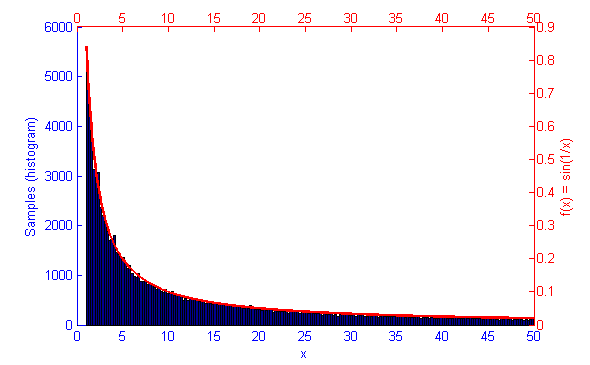
However, if the function f(x) represents a curve then the number of samples in high energy (probability) regions needs to be more dense. This can be seen in the simulations of f(x) = sqrt(x-1) and f(x) = sin(1/x) below.
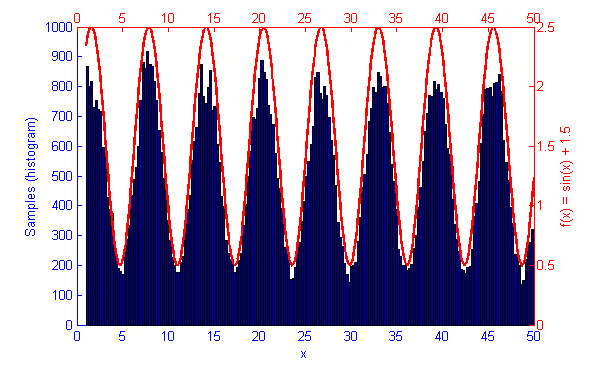
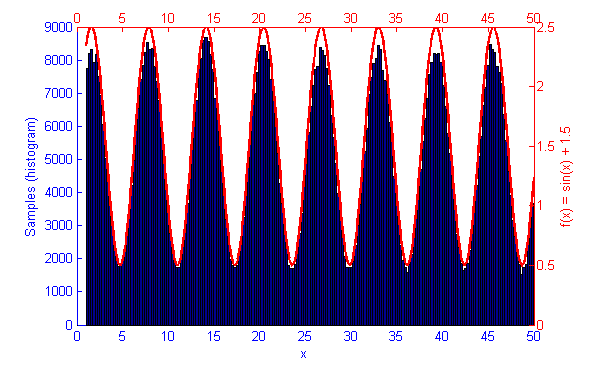
Metropolis-Hastings is best suited to problems where Direct Sampling and other more efficient solutions are not available. Because it only relies on the availability of a computable function f(x) and a proposal density Q(x|x*) M-H can correctly sample unusual probability distributions that would else-wise be difficult or impossible to compute. This can be seen below in the simulations of the sine function f(x) = sin(x) + 1.5.
Matlab code for Metropolis-Hastings Monte Carlo Integration (for generating samples)
Below is the Matlab code used to generate the above graph. By modifying the function f(x), the sample count N, the proposal distribution and it’s variance qV, and the upper and lower truncation bounds LB & HB any PDF can be simulated.