Program The rantings of a lunatic Scientist

Posts by Joss Whittle

Auxiliary Classifier – Generative Adversarial Networks in Keras

April 12, 2017 - 3:51 pm by Joss Whittle GPGPU Graphics Keras Machine Learning PhD Python

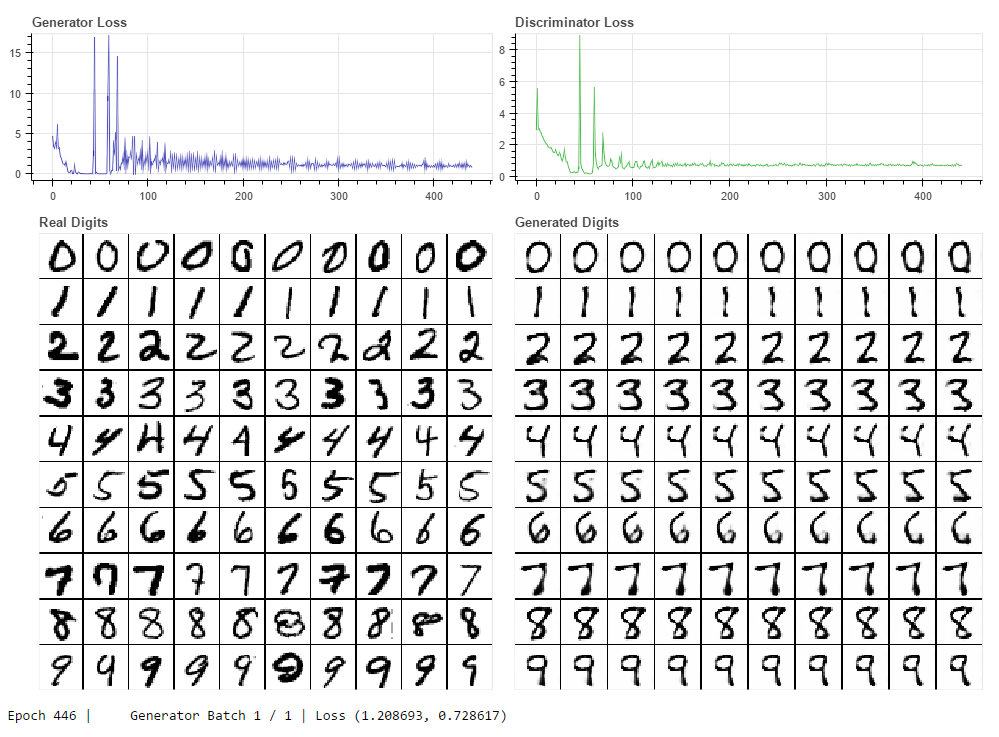
An experiment in augmenting a GAN architecture to use class-labels to guide image synthesis. The generator network takes as input a vector of 1 x 10 random values to use a seed for image synthesis, and a 1 x 10 one-hot vector for the class-label representing the desired digit.

In the above image the generated digits are made by giving the same 1 x 10 random vector for each image, with the y-axis varying the class-label, and the x-axis sweeping the value of one (common to all rows) randomly chosen column in the random vector between [0,1).

Farming for Pixels – A teaching lab becomes a computational cluster

April 26, 2015 - 5:41 pm by Joss Whittle C/C++ Graphics PhD

While working on my submission to this years SURF Research as Art Competition I realized that if I was to have any hope of rendering the final image at high resolution in a reasonable amount of time I would need more power. To do this I applied node parallelism in the form of a computer lab turned render farm.

The above image is the result of ~8 hours of rendering, at 4k resolution, over 18 machines (as described below). No colour correction or other post-processing (other than converting to jpeg for uploading) has been applied.

I try to keep the current generation of my rendering software nicely optimized but at it’s core it’s purpose is to be mathematically correct, capable of capturing a suite of internal statistics, and to be simple to extend. Speedup by cpu parallelism is only performed at the pixel (technically pixel tile) sampling level to reduce the amount of intrusion ray-packet tracing can bring to a renderer. In the future I plan to add a GPU work distributor using CUDA but for now this is quite low on my research priorities.

In order to get the speed boost I needed to render high resolution bi-directional path traced images I made use of Swansea Computer Sciences – Linux Lab, which has 30 or so i7, 8GB Ram, 256GB SSD machines running OpenSUSE. I wrote a bash script which for each ip address in a machine_file (containing all ip’s in the farm) ssh’s into each system and starts the renderer as a background process, and another to ssh into all machines and stop the current render.

The render job on each node outputs to a unique binary partials file every 10 samples per pixel (at 4k resolution) to a common network directory, overwriting the files previous values. This file contains three int’s containing width, height, and samples respectively; followed by (width * height * 3) double precision numbers representing the row-column pixel data stored in BGR format.

The data in the file represents the average luminance of each pixel in HDR. A second utility program can be run at a later time to process all compatible partials files in the same directory and turn them into a single image. Which is then properly tone mapped, gamma corrected, and saved as a .bmp file. To combine two partials, the utility program simply performs the following equation for each pixel:

P_1,2 = ((P_1 * S_1) + (P_2 * S_2)) / (S_1 + S_2)

By repeating this process one by one (each partial file can be > 500MB) all partials in a directory can be aggregated together into a single consistent and unbiased image.

Tags Bi-Directional Path Tracing, Concurrency, Depth of Field, Global Illumination, Maya, Path Tracing

An ode to Pixar Renderman’s — Physically Plausible Pig

March 8, 2015 - 8:35 pm by Joss Whittle C/C++ Graphics PhD

After succumbing to a bit of a slump in research productivity over the last week or two it feels great to be making progress again.

Finally I have a fully functional implementation of Bidirectional path tracing with some basic multiple importance sampling for the path weights. To celebrate having this new renderer in the code base I decided to have another crack at implementing a ceramic like shader. In the past I had modeled this material in geometry by placing a diffuse textured sphere inside an ever so slightly larger glass sphere to model the glaze/polish of the material. However, this method was a clunky approximation and severely limited the complexity of the models which it could be applied to.

This time I modeled a blended BRDF between a lambertian diffuse under-layer and an anisotropic glossy over-layer to represent the painted ceramic glaze. The amount of each BRDF used for each interaction is modulated by a Fresnel term on the incident direction. This means that looking straight at the surface will show mostly the coloured under-layer, while looking at glancing angles will show mostly the glossy over-layer.

The final, most important, part of this shader however is the bump map applied to it. Originally I rendered this scene without bump mapping, and while the material seemed plausible it looked almost too perfect. To break up the edges of reflections and to allow the surface of the material to “grab” onto a bit more light the effect of the material becomes and order of magnitude more convincing.

Tags Bi-Directional Path Tracing, Depth of Field, Global Illumination, Monte Carlo Integration, Path Tracing

Concentric Disk Sampling

December 22, 2014 - 10:49 am by Joss Whittle C/C++ Graphics Maths for Comp Sci Matlab PhD University

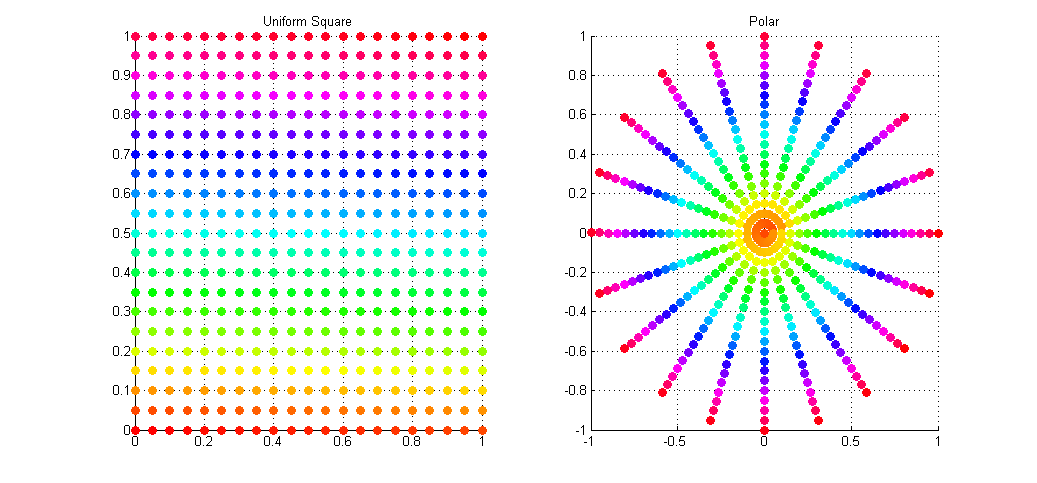
Yesterday I stumbled upon a lesser known and far superior method for mapping points from a square to a disk. The common approach which is presented to you after a quick google for Draw Random Samples on a Disk is the clean and simple mapping from Cartesian to Polar coordinates; i.e.

Given a disk centered origin (0,0) with radius r

// Draw two uniform random numbers in the range [0,1)
R1 = RAND(0,1);
R2 = RAND(0,1);

// Map these values to polar space (phi,radius)
phi = R1 * 2PI;
radius = R2 * r;

// Map (phi,radius) in polar space to (x,y) in Cartesian space
x = cos(phi) * radius;
y = sin(phi) * radius;

The result of this sampling on a regular grid of samples is shown in the image below. The left plot shows the input points as simple ordered pairs in the range [0,1)^2, while the right plot shows these same points (colour for colour) mapped onto a unit disk using Polar mapping as described above.

As you can see the mapping is not ideal with many points being over-sampled at the poles (I wonder why they call is Polar coordinates), and with areas towards the radius left under-sampled. What we would actually like is a disk sampling strategy that keeps the uniformity seen in the square distribution while mapping the points onto the disk.

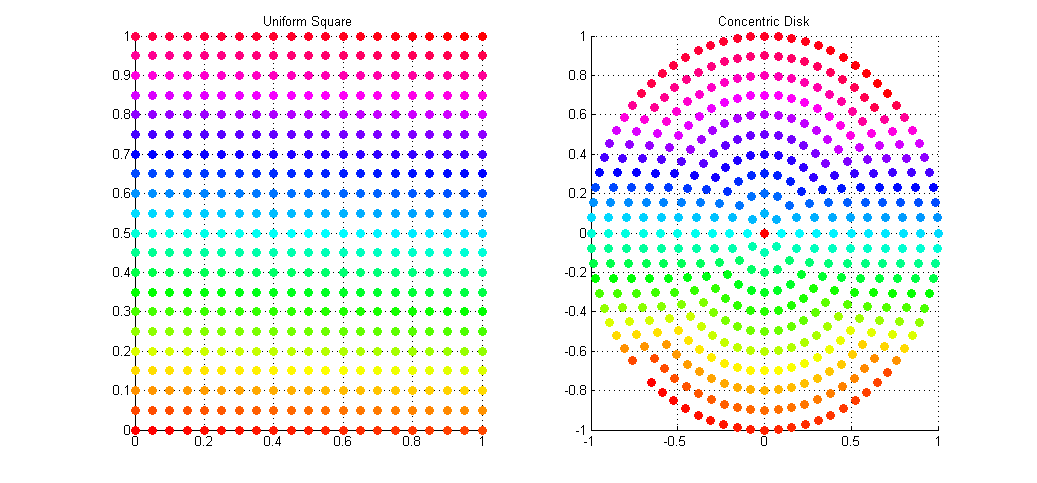
Enter, Concentric Disk Sampling. This paper by Shirley & Chiu presents the idea for warping the unit square into that of a unit circle. Their method is nice but it contains a lot of nested branching for determining which quadrant the current point lays within. Shirley mentions an improved variant of this mapping on his blog, accredited to Dave Cline. Cline’s method only uses one if-else branch and is simpler to implement.

Again, given a disk centered origin (0,0) with radius r

// Draw two uniform random numbers in the range [0,1)
R1 = RAND(0,1);
R2 = RAND(0,1);

// Avoid a potential divide by zero
if (R1 == 0 && R2 == 0) {
    x = 0; y = 0;
    return;
}

// Initial mapping
phi = 0; radius = r;
a = (2 * R1) - 1;
b = (2 * R2) - 1;

// Uses squares instead of absolute values
if ((a*a) > (b*b)) { 
    // Top half
    radius  *= a;
    phi = (pi/4) * (b/a);
}
else {
    // Bottom half
    radius *= b;
    phi = (pi/2) - ((pi/4) * (a/b)); 
}

// Map the distorted Polar coordinates (phi,radius) 
// into the Cartesian (x,y) space
x = cos(phi) * radius;
y = sin(phi) * radius;

This gives a uniform distribution of samples over the disk in Cartesian space. The result of the mapping applied to the same set of uniform square samples is shown above. Notice how we now get full coverage of the disk using just as many samples, and that each point has (relatively) equal distance to all of it’s neighbors, meaning no bunching at the poles, and no under-sampling at the fringe.

I’ve applied this sampling technique to my Path Tracer as a means of sampling the aperture of the virtual point camera when computing depth of field. Convergence to the true out-of-focus light distribution is now much faster and more accurate than it was with Polar sampling which, due to bunching at the poles, cause a disproportionate number of rays to be fired along trajectories very close to the true ray.

Tags Depth of Field, Path Tracing

Uniform random numbers? We can do better…

June 30, 2014 - 8:35 pm by Joss Whittle C/C++ Graphics Matlab PhD

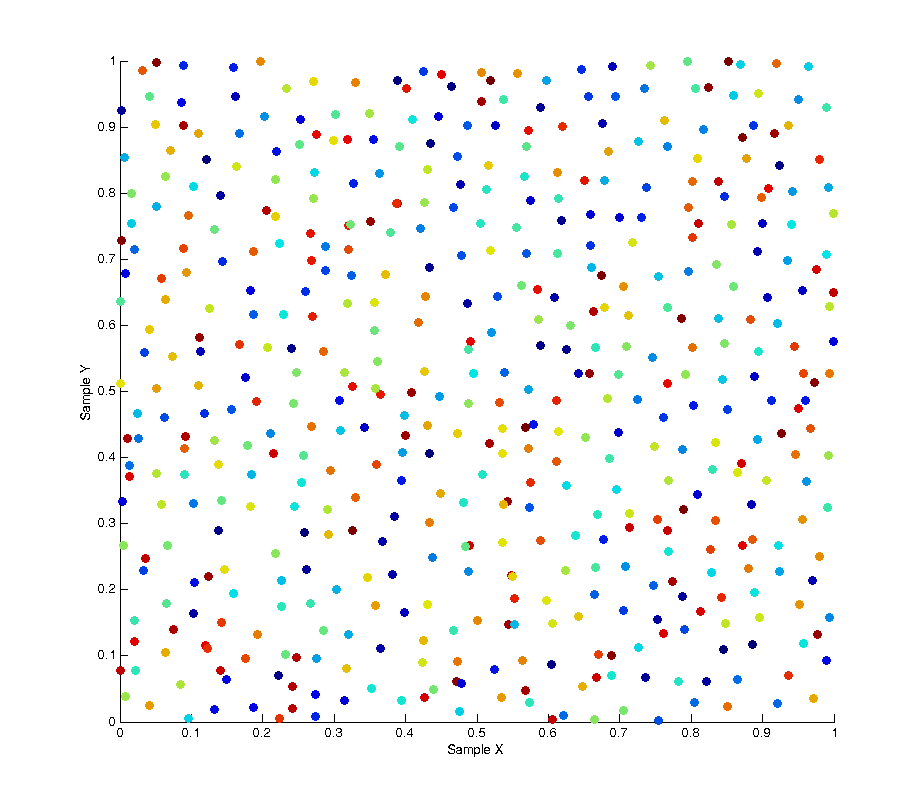
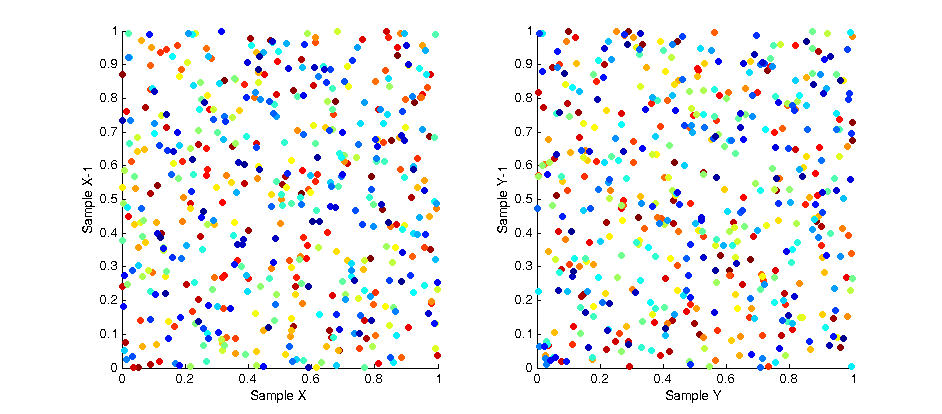
In monte carlo rendering we need random numbers. Like… a lot of random numbers. In fact if you count every call to the random functions in a single render it can easily surpass a several million numbers. Not only do we need lots of numbers, but we tend to need ones which have certain desirable properties such as proper uniformity without accidental bunching. To explain the problem being addressed, the image below shows 500 “uniform” random samples over a [0.0, 1.0] square, where the colour of each sample refers to its order throughout the sampling (blue -> red). As you can see the result of this leads to bunching and poor distribution over the entire sample space with some areas being under-sampled and some areas over-sampled. In the use case of image anti-aliasing this can lead to duplication of expensive computations on similar sub-pixels while other areas of the pixel space get left un-sampled.

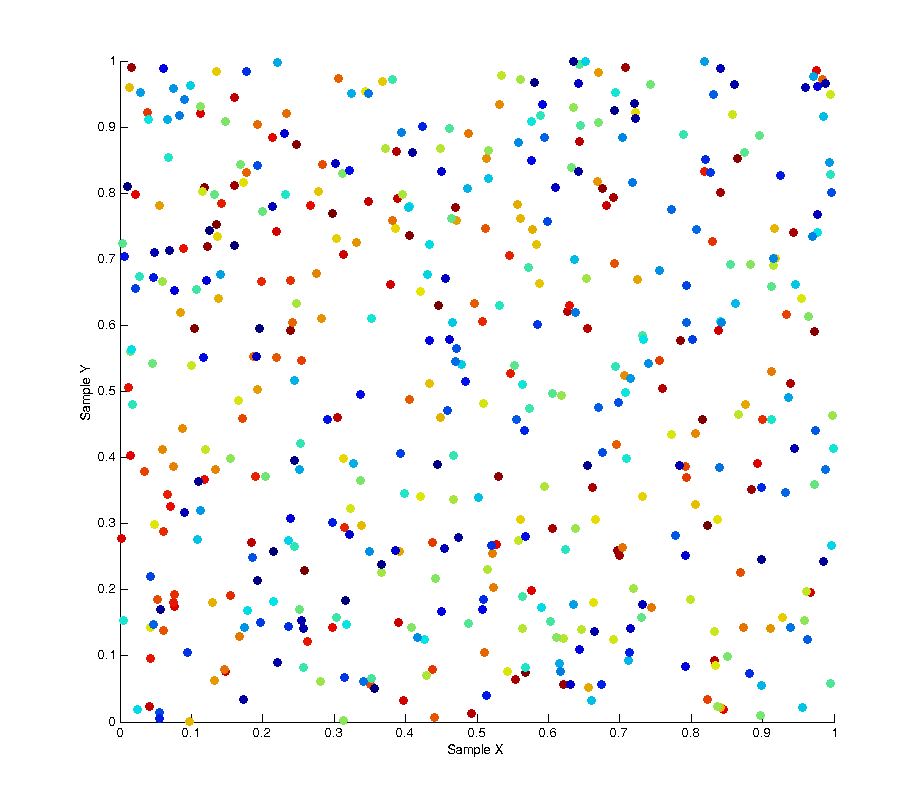
One possible solution to this is Poisson Disk Sampling which aims to solve the problem of sample distribution by creating a whole batch of samples at once where each sample is at least a minimum distance from any other sample. Because samples have to be generated in batches this leads to a high correlation between samples due to the fact that after an initial “seed” sample is chosen all subsequent ones are the product of growing outwards from this seed. As can be seen in the image below Poisson sampling gives a nice, lamina, distribution of samples over the sample space. The below image is the product of 500 samples of Poisson sampling with a minimum distance of 0.05. At this distance setting the sampling tends to generate samples in batches of approximately 400 samples, whenever the list of batched samples is depleted a new batch is produced.

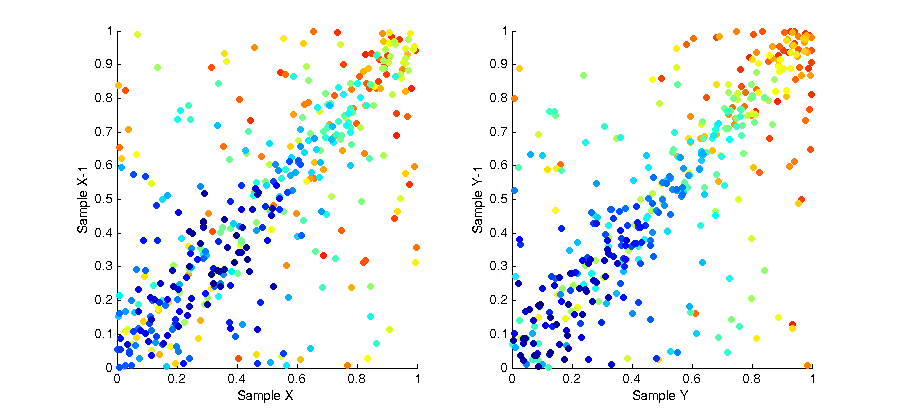
While the overall distribution of samples appears lamina, the intermediate distribution at any discrete interval throughout the sampling is not. This is due to the fact samples are “grown” in batches. The image below shows the affect of this correlation by plotting the X and Y values of each sample with respect to the X and Y values of the previous samples. As you can see a strong pattern emerges across each axis.

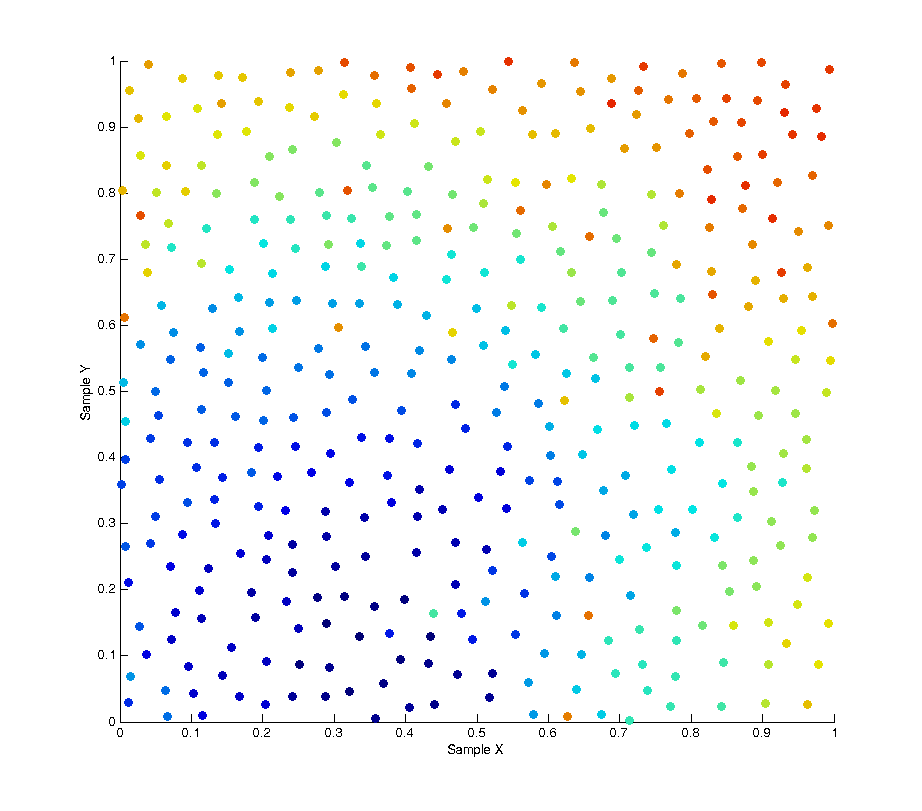
To remove this bias we can use a technique called a “random pop” to select elements from within each batch uniformly rather than in sequence. At each sample we select a random element from the batch, then copy the last element of the list into that spot and pop the last element from the list before returning the random element we selected. The result of this solution is that at any point within a given batch of samples the distribution of samples is uncorrelated and unbiased. This is shown in the image below, as you can see the colour of each sample is now randomly distributed.

By plotting the correlation between samples again we can also see there is no pattern across the whole set of samples.

Tags Poisson, Sampling, Uniform